Åren 1950 till 2017 ökades penningmängden från 24 miljarder till 3235 miljarder kronor. 2017 fanns det alltså 135 gånger fler kronor än 1950 och om inget annat ändrats skulle priserna ökat till att vara 135 gånger högre nu än 1950.
 Penningmängden ökas så kraftigt att vi behöver logaritmisk skala för att kunna se detaljer i hela tidsintervallet.
Penningmängden ökas så kraftigt att vi behöver logaritmisk skala för att kunna se detaljer i hela tidsintervallet.

 Penningmängdsmåttet M3 är enkelt uttryckt summan av alla kontanter och bankkonton och har under lång tid ökats med i genomsnitt 7.5% per år. 7.5% och 135 gånger låter mycket men här följer en snabb rimlighetskoll. Hårklippning är en tjänst som inte ändrats mycket sedan 1950-talet. Tiden en klippning tar är fortfarande densamma och verktygen är också ungefär desamma. 1954 kostade en herrklippning runt 2.90 kr och 400 kr är ett normalt pris idag. Skor, som kan antas ha haft en viss produktivitetsökning, har sedan 1951 ändå ökat uppemot hundra gånger i pris.
Penningmängdsmåttet M3 är enkelt uttryckt summan av alla kontanter och bankkonton och har under lång tid ökats med i genomsnitt 7.5% per år. 7.5% och 135 gånger låter mycket men här följer en snabb rimlighetskoll. Hårklippning är en tjänst som inte ändrats mycket sedan 1950-talet. Tiden en klippning tar är fortfarande densamma och verktygen är också ungefär desamma. 1954 kostade en herrklippning runt 2.90 kr och 400 kr är ett normalt pris idag. Skor, som kan antas ha haft en viss produktivitetsökning, har sedan 1951 ändå ökat uppemot hundra gånger i pris.
Inflationen av penningmängden är inte det enda som påverkar en varas prisutveckling. Produktivitetsutveckling och pengars omsättningshastighet är två andra saker som kan ha stor betydelse. Som synes har dock omsättningen ökat ungefär lika mycket som penningmängden både i närtid och under hela tidsperioden sedan 1950 så i fortsättningen kan vi bortse från den.
 Produktivitetsutvecklingen, eller tillväxten, då? Real BNP är ett index över hur mycket som producerats. Man väljer ett basår och räknar antalet tillverkade brödrostar, cyklar, m.m. varje år och multiplicerar med basårets priser. På så sätt får man en siffra på ungefär hur mycket som producerats ett år jämfört med ett annat år. Tillverkades en brödrost första året och två brödrostar andra året blir real BNP helt enkelt 1 respektive 2.
Produktivitetsutvecklingen, eller tillväxten, då? Real BNP är ett index över hur mycket som producerats. Man väljer ett basår och räknar antalet tillverkade brödrostar, cyklar, m.m. varje år och multiplicerar med basårets priser. På så sätt får man en siffra på ungefär hur mycket som producerats ett år jämfört med ett annat år. Tillverkades en brödrost första året och två brödrostar andra året blir real BNP helt enkelt 1 respektive 2.
Konsumentprisindex (KPI) är ett index över hur samma varor förändras i pris över tid. Produktivitetstillväxt har en sänkande effekt på varornas pris. Så om penningmängden dubblas men tillverkarna av brödrostar kan göra dubbelt så många brödrostar med samma mängd resurser leder det inte till någon ökning av KPI. Priset förblir konstant men skulle halverats utan uppblåsningen av penningmängden.
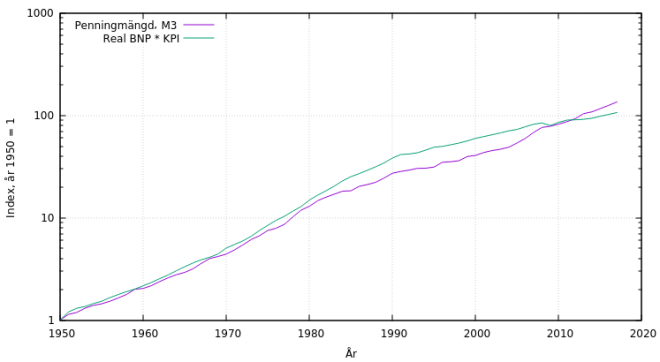
 Detta är en stor orsak till att ökningstakten för KPI är långt under inflationstakten för penningmängden. Om vi multiplicerar KPI med ökningen för real BNP bör vi hamna närmare utvecklingen för M3.
Detta är en stor orsak till att ökningstakten för KPI är långt under inflationstakten för penningmängden. Om vi multiplicerar KPI med ökningen för real BNP bör vi hamna närmare utvecklingen för M3.
 Staten – som tar fram statistiken – har dock starka incitament att underdriva KPI och överdriva tillväxten. Samtidigt är det ett stort mått av godtycke och mänskliga bedömningar inblandat i att ta fram siffrorna. Så man kan befara att det verkliga förhållandet mellan prisökningar och tillväxt är något annorlunda, men det är ett ämne för ett senare tillfälle.
Staten – som tar fram statistiken – har dock starka incitament att underdriva KPI och överdriva tillväxten. Samtidigt är det ett stort mått av godtycke och mänskliga bedömningar inblandat i att ta fram siffrorna. Så man kan befara att det verkliga förhållandet mellan prisökningar och tillväxt är något annorlunda, men det är ett ämne för ett senare tillfälle.
KPI är till exempel användbart till att indexera pensionsutbetalningar så att de köper en någorlunda konstant absolut levnadsstandard. En sådan pensionär blir dock hela tiden fattigare relativt resten av samhället allt eftersom ekonomin växer och andra blir rikare. I en ekonomi med fast penningmängd som exempelvis en framtida Bitcoin-ekonomi så skulle en sådan KPI-indexerad pension sänkas även nominellt när ekonomin växer.
 Samma sak gäller förstås löner. Alla löneökningar under 7.5% är lönesänkningar. Löntagarens andel av köpkraften blir då mindre än året innan. Med fast penningmängd skulle den nominella lönesumman, alltså antalet kronor i månaden, behöva sänkas för att uppnå samma resultat.
Samma sak gäller förstås löner. Alla löneökningar under 7.5% är lönesänkningar. Löntagarens andel av köpkraften blir då mindre än året innan. Med fast penningmängd skulle den nominella lönesumman, alltså antalet kronor i månaden, behöva sänkas för att uppnå samma resultat.
Lönerna har följt inflationen ganska länge men har på senare år halkat efter till att numera vara mindre än hälften så höga relativt penningmängden jämfört med 1950.
 Alla räntor under 7.5% är negativa räntor. Varje mängd pengar som ackumulerar ränta på ränta lägre än 7.5% kommer, om pengaskapandet fortsätter i samma takt, med tiden gå mot ett värde av noll brödrostar. Ett vanligt bankkonto med 0% ränta tappar hälften av sin relativa köpkraft på tio år. Tillsammans med 30% skatt på den nominella avkastningen när sådan finns får detta effekten att det blir mycket oattraktivt att spara pengar. Ett vanligt bostadslån med nominell ränta på 1.5% har en reell ränta på -5.6%. Tillsammans med ränteavdrag är detta anledningen till att så många lånar sådana enorma mängder rykande färska pengar.
Alla räntor under 7.5% är negativa räntor. Varje mängd pengar som ackumulerar ränta på ränta lägre än 7.5% kommer, om pengaskapandet fortsätter i samma takt, med tiden gå mot ett värde av noll brödrostar. Ett vanligt bankkonto med 0% ränta tappar hälften av sin relativa köpkraft på tio år. Tillsammans med 30% skatt på den nominella avkastningen när sådan finns får detta effekten att det blir mycket oattraktivt att spara pengar. Ett vanligt bostadslån med nominell ränta på 1.5% har en reell ränta på -5.6%. Tillsammans med ränteavdrag är detta anledningen till att så många lånar sådana enorma mängder rykande färska pengar.
Datakällor
M3, 1846-2012 (Volym 2, kapitel 7)
M3, 1981-2017
KPI
Löner 1861-1988
Löner 1991-2017



Intressant analys, tack!
(Och för ovanlighetens skull i ekonomisammanhang även korrekt procenträkning).
Skulle du kunna jämföra även med statens (ofentlig sektors) tillväxt under perioden?
GillaGilla
Tack! Offentliga sektorns tillväxt är intressant i sig själv men hur ska den relateras till inflationen?
GillaGilla
[…] Länk till inlägget: https://dberntsson.info/2018/05/04/inflationens-dolda-storlek/ […]
GillaGilla
Grymt sade grisen. Något jag misstänkt, men inte lagt något krut på att ta reda på, tack!
GillaGilla
Riktigt bra analys, tack för den!
En liten detalj bara, angående sista meningen om ”rykande färska riksbankspengar”:
Det är inte riksbankspengar man lånar, utan det är pengar skapade av privatbankerna.
Man kan inte ha riksbankspengar på sitt bankkonto. Riksbankspengar kan (med undantag av kontanter) bara hanteras av storbankerna. Man måste ha konto i RIX för att kunna inneha riksbankspengar.
Det är till största delen privatbankerna som skapar de nya pengar som blåser upp M3.
GillaGilla
Bankerna lånar nya pengar av Riksbanken och lånar i sin tur ut dem till sina kunder. Sedan multipliceras pengarna när de upprepade gånger lånas in och ut ur bankerna och man använder fordringar på bankerna (”pengar på kontot”) som pengar.
GillaGilla
Det är det som privatbankerna vill få oss att tro, men så är det inte.
Privatbankerna lånar inte ut de pengar de lånar av riksbanken, det är inte samma pengar.
Privatbankerna måste ha en viss kapitaltäckningsgrad, dvs de måste inneha riksbankspengar för att kunna få skapa nya pengar, men det är bara en liten del av hur mycket pengar de tillåts skapa.
Om du tar ett lån på en bostad från en privatbank så skapas summa pengar du lånar i samma ögonblick som lånet tas. M3 ökar med samma belopp.
Här är ett citat från Stefan Ingves:
===============================
”Ett exempel kan belysa vad kapitaltäckningsreglerna tillät och fortfarande tillåter. Antag att vi har en husköpare som lånar 1 miljon kronor och belånar sitt hus till 100 procent. Riskvikten för bolån kan vi uppskatta till 10 procent. I så fall blir de riskvägda tillgångarna för lånet 100 000 kronor. Det totala kapitalkravet är på 8 procent, vilket innebär att banken måste hålla kapital på 8 000 kronor. Det mer relevanta primärkapitalkravet är 4 procent, så primärkapitalet måste motsvara 4 000 kronor. Av primärkapitalet kan 30 procent vara hybrider av olika former. Det innebär att en bank kan komma undan med ett eget kapital – riktigt aktiekapital och upparbetade vinster – på 2 800 kronor för en utlåning på 1 miljon kronor. Ger 2 800 kronor i förlustabsorberande kapital tillräcklig motståndskraft vid utlåning på 1 miljon kronor?
Mitt svar är nej”
===============================
Klicka för att komma åt 091119.pdf
GillaGilla
Här förklaras hur det går till:
GillaGilla
Se även:
GillaGilla
Du har rätt. Jag har ändrat till bara ”pengar”. Här är en mycket bra skrift om ämnet: https://www.bankofengland.co.uk/-/media/boe/files/quarterly-bulletin/2014/money-creation-in-the-modern-economy.pdf
GillaGilla
”Produktivitetsutveckling och pengars omsättningshastighet är två andra saker som kan ha stor betydelse. Som synes har dock omsättningen ökat ungefär lika mycket som penningmängden både i närtid och under hela tidsperioden sedan 1950 så i fortsättningen kan vi bortse från den.”
Omsättningshastigheten för pengar – hur ofta en sedel omsätts, eller går runt, i ekonomin – påverkar inflationen, ja. Men på motsatt sätt. Om omsättningshastigheten går up så ökar priserna, även om de går upp tillsammans med penningmängden.
Såhär, det här är kvantitetstekvationen, som jag tror Milton Friedman formaliserade…eller populariserade (han hade den som registreringsskylt för sin bil).
MV = PQ
Money supply * Velocity of money = Price Level * Quantity of Goods
https://en.wikipedia.org/wiki/Equation_of_exchange
Så, P = MV/Q. Om kvantiteten av alla varor ökar, så minskar priserna. Men om pengamängden eller pengahastigheten ökar så ökar priserna också. De tar alltså inte ut varandra utan går i samma riktning.
Så, en del av ökningen i P beror på ökningen i V. Dock har jag hört att Friedman argumenterade för att V i princip är konstant – han kollade på 1880-1960 ungefär. Ett halvdant sätt att mäta det på är hur mycket pengar man själv håller i plånboken och som inte kan lånas ut (pengar i banken sätts i normalfall i rörelse, men det finns ju undantag som åren efter senaste krisen). Rimligtvis borde då V stigit något de senaste 40 åren, och särskilt de senaste 15 åren, iom att bankkorten tagit över mer och mer av vardagstransaktionerna.
”KPI är till exempel användbart till att indexera pensionsutbetalningar så att de köper en någorlunda konstant absolut levnadsstandard. En sådan pensionär blir dock hela tiden fattigare relativt resten av samhället allt eftersom ekonomin växer och andra blir rikare. … Samma sak gäller förstås löner. Alla löneökningar under 7.5% är lönesänkningar. Löntagarens andel av köpkraften blir då mindre än året innan.”
Då borde det ju även vara okej att säga att de rika blir rikare och de fattiga blir fattigare, om fattigdom och rikedom är relativa begrepp gentemot alla andra i ekonomin. Så, en arbetare var fattigare 1950 än 1850, då de rikare var mycket rikare då.
Men, det här argumentet missar att i en ekonomi som växer ekonomiskt och befolkingsmässigt så är det naturliga att varje individs del minskar ständigt. En arbetare – eller en kapitalist – som får googol av allt värde 1800, får en tiondels googol år 1900. Så, om bara befolkningsmängden ökar så kommer alla, enligt den här definitionen, få lönesänkningar och bli fattigare, även om de lever i slott.
Ett sätt att empiriskt kolla om det är rimligt är att ta folks medellön förr och se hur mycket de skulle tjäna nu. Så, en genomsnittsarbetare tjänade 20 300 år 2001 enligt LO. Med 7% löneökning varje år så skulle lönerna gå upp ca 3.,16 ggr. D.v.s. denne hade tjänat 64 000 kr, en betydlig löneökning som hade stått emot huspris- och bensin/skatteökningarna (typ 3 ggr och 2 ggr pengarna vardera, ungefär).
Klicka för att komma åt Loner2001.pdf
https://www.ekonomifakta.se/Fakta/Ekonomi/Hushallens-ekonomi/Bostadspriser/
Samma gäller ränta. En dryg miljon köper dig ett hus 2001. Med 7% ränta får man kanske 3,2 miljoner nu och då kan man köpa ungefär samma hus, Och det är väl husen som gått upp mest i pris, så allt annat hade ju definitivt blivit billigare.
https://www.zerohedge.com/news/2016-03-16/sweden-most-risk-asset-bubble-moodys-warns-after-taking-look-swedish-house-prices
Annars, jag litar inte på Riksbankens mått av M3, men vad annars kan man utgå ifrån, om något borde de väl förminska ökningen, men det verkar de inte ha brytt sig om?
GillaGilla
MV = PQ är inte ett korrekt mått på omsättningshastigheten. Motbevisades redan på 90-talet. http://www.postkeynesian.net/downloads/Werner/RW301012PPT.pdf
GillaGilla
[…] Sveriges vanliga vinstskattesats på 30% och en vanlig inflation av penningmängden med 7.5% per år blir den faktiska förmögenhetsskatteeffekten 0.075 * 0.3 = 0.0225, över 2%. Skatteeffekten av […]
GillaGilla